
 |

| In the symbolism shown,
(a) the Centerpoint represents the center of Mars, (b) the Wedge represents the surface,
(c) the Face represents the moon Phobos, and (d) the Second Face represents the moon
Deimos. Distances are aligned on a straight line to the same scaled proportions of the
Martian moon system. The Centerpoint, with its 'dots' arranged in a square, is a variation of the 'cross-hairs' symbol found universally on schematic diagrams to designate the center of a circle. It serves the same purpose in the Cydonia Complex. Moving to the right in Figure 6, we come to the rock formation dubbed the 'Wedge.' Rather than build an entire ring at backbreaking expense, the Martians chose to depict the cross-section of the Martian planetary surface with a smaller 'distance marker'monument instead. Continuing eastward, we come to the Faces. As in Earth tradition, a face is used to symbolize a moon. The First Face represents Phobos, the Second Face is Deimos. So there are four symbols -- Centerpoint, Wedge, Face, and Second Face. Each is symbolically appropriate for its role in a schematic diagram representing the Martian moon system: 1. Centerpoint = Cross-hairs marking center of planet and orbits. 2. Wedge = border segment marking surface of Mars. 3. Face = anthropomorphic symbol for inner moon, Phobos. 4. Second Face = anthropomorphic symbol of outer moon, Deimos. And to be a schematic diagram, the distances must be proportional to the same scale: 1. Centerpoint-Wedge = Radius of Mars. 2. Centerpoint-Face = Orbital radius of Phobos. 3. Centerpoint-Second Face = Orbital radius of Deimos. And this is indeed the case. Even a simple astronomy book will confirm the numbers for the radius of Mars and the orbits of its moons. If you can work with a calculator and a ruler, you can compare distances in the composite photograph. The measured distances are within one percent of the predicted values. Another numerical correspondence between moons and monuments has to do with the location of the Cydonia Complex. Our Martian moon god priest wants the best location for the Cydonia Complex. That location would be the one with the best view. Is there a way to determine the best view mathematically? For longitude, the answer is no. Longitude is measured from an arbitrary point on the surface. Latitude, however, is measured from the equator, and is objectively assigned. On a globe, latitude is the angle between the location and the equator, measured from the center. The equator has a latitude of zero. The poles have a latitude of ninety degrees. All other possible latitudes fall within this range. The best viewing latitude is described in Figure 7. Figure 7: Latitude Relationship
(A) Latitude is a means of mathematically locating a position on a planet. Point X is at latitude A North, where the latitude is equal to the angle A with respect to the equator and the center of the planet. |
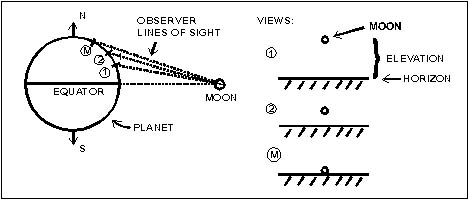
| (B) Suppose a moon orbits over the equator. As an observer moves poleward, the apparent elevation of the moon relative to the horizon becomes less. At latitude M the moon rises no higher than the horizon, and above this latitude the moon cannot be seen at all. |
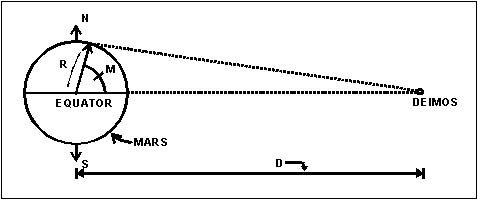
| (Distances and angles are
NOT to scale!) (C) Where: M = Maximum latitude at which Deimos can be seen from surface of Mars. R= Planetary radius of Mars D = Orbital radius of Deimos Using simple trigonometry, we can determine latitude M as M = ArcCos(R/D) = (3397km/23,500km) = 82 degrees (approx) for Mars and Deimos. This is almost exactly twice the latitude of the Cydonia Complex. At the equator, the moons pass directly overhead. This isn't good -- for observers on the ground, participating in religious ceremonies, there's neck strain, and for the 'moon gods,' one moon passes in front of the other at zenith, blocking the 'god's view.' So the equator is ruled out as a place to locate the temple. How about the poles? Actually, neither moon can be seen at the poles. The curvature of the planet gets in the way. The maximum latitude at which the outer moon, Deimos, can be seen is 82 degrees. At that latitude, Deimos pops over the horizon only briefly once every three days, and Phobos cannot be seen at all. This is hardly optimal for a temple meant to serve these moon gods! How about a compromise, then? Instead of the equator, or the maximum latitude of 82 degrees, why not the latitude which is exactly in the middle? The average of the equatorial and maximum latitudes would be: (0 + 82)/2 = 41 degrees. And that is the officially-designated latitude which NASA has identified for the Cydonia Complex, as mentioned in public literature[2] and on the data captions of the official Viking photographs themselves. As with the distances, the actual latitude corresponds to theory-predicted value within one percent. Let's do a third correspondence. This one relates the angle of the lunar orbital plane with respect to the planetary orbital plane, and the tilt of the Cydonia Complex with respect to the equator of Mars. This is one of those things that makes very little sense in words, but is understandable enough in pictures. The pictures are shown in Figures 8. As can be seen, the Martian priests designed the Cydonia Complex to mimic the motion of the Martian moon system as Mars orbits the Sun! Figure 8: Inclination Relationship |

| (A) Mars orbits the sun as
a planet, while Phobos and Deimos orbit Mars as moons. (Note: orbital distances are not to
scale!)
(B) The axial tilt of a planet is defined as the angle between the polar axis and the line perpendicular to the orbital plane. For Mars, the axial tilt is 24 degrees.
(C) It is a property of planetary geometry that the angle between the equator and the orbital plane is equal to the axial tilt -- again, 24 degrees.
(D) The orbital plane of Deimos around the planet Mars is tilted at 1.8 degrees with respect to the equator of Mars. Thus, the maximum tilt of the orbit of Deimos with respect to the orbital plane of Mars is 24 + 1.8 = 26 degrees (approx.). (E) At the Cydonia Complex, the Centerpoint and 'Moon Monuments' are at a slope of 26 degrees with respect to a line running due east. |
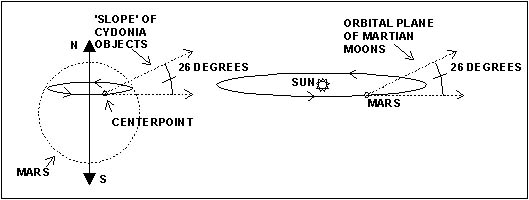
| (F) As Mars rotates on its
axis, the Cydnoia Complex 'orbits' around the axis. This is symbolic of Mars orbiting the
Sun. Likewise, the 'slope of the Cydonia Complex' with respect to its 'orbit' is symbolic
of the inclination of the Martian moon system with respect to the orbital plane of Mars. Described in words, the concept may seem esoteric, but in fact, axial tilt is a basic quantity which is found in the most simple books on astronomy. Since axial tilt determines the changing of seasons, pre-industrial agricultural societies were acutely aware of its influence. The Martians would think it is important, too, and so they would incorporate it in their most important temple. The axial tilt of Mars is a very public number, and can be readily found in many astronomy books -- though, for reasons unknown, some say it is 24 degrees and others say it is 25.2 (either way the correspondence is within one percent). The Cydonia 'slope' can be measured off the NASA photographs. The Cydonia faces are aligned on the same line with respect to the Centerpoint. This suggests that the orbital planes of the Martian moons are tilted the same amount with respect to the orbital plane of Mars. Actually, they differ by about a degree. This is a minor disagreement, as we shall see, and furthermore there is good reason to believe that at one time the moon orbits were aligned. There are other relationships, but these are the ones easiest to measure and correlate. They are not based on esoteric, arbitrary attributes, but on basic data about the moons that can be found in a typical book on popular astronomy. With such a book, and a ruler, and protractor, and calculator (and perhaps with the photographs ordered from NASA if you don't trust the reproductions here), you can verify all of these relationships on your own. No advanced degree in science or mathematics is required to do this. So many correspondences should strengthen the case that the Cydonia Complex is artificial. And no one can say, "The human mind has a natural propensity to imagine Martian moon systems." Faces, perhaps. Moon systems, no. But -- is it likely, or unlikely, that the Cydonia Complex is a model of the Martian moon system? Can we quantify a probability?
Let's quantify the critic's case first. Relevant to the Face alone, Carl Sagan has commented:
This is an appeal to intuition, but it's a powerful one. Even if the Face on Mars is one in a million, Mars has 150 million opportunities to generate it randomly. By itself, the Face cannot overcome the argument from chance. But we haven't been looking at just the Face. We've been looking at the Cydonia Complex, which is more complex and numerically precise than a single image of a face. The surface area of Mars is 150 million square kilometers. The Cydonia Complex is roughly ten kilometers by sixty. At 600 square kilometers, the Cydonia Complex is 250,000 times smaller than the surface area of Mars. We could mentally divide the surface of Mars into a grid with 250,000 cells, each the size of the Cydonia Complex. In a sense, each one of these cells represents a 'try' for Mars to randomly produce the Cydonia Complex, by geological and meteorological forces alone. In other words, because of its size, Mars has 250,000 opportunities to reproduce the images, distances, and angles we see at Cydonia. The critics imply 250,000 chances are enough to do this. But let's see what the numbers actually say. The first numbers we developed with respect to distances between the monuments and those of the moon system. Three distances were involved. One distance, however, was used to define the scale. Coincidence came when the other two distances agreed with that scale, within one percent. Now, what is the probability of that happening by pure chance? Let's divide the line between the Centerpoint and the predicted scale distance into a hundred equal slots. In only one of these slots are we within one percent of the predicted distance. What is the probability that a landform would randomly fall in that slot? Since the slot is one out of a hundred, the probability is only 1/100. So there is 1/100 probability the Face would end up where it did. The Second Face is another 1/100 probabilty. The latitude of the Cydonia Complex was also within one percent of the predicted value. That's another 1/100 probability. Then there was the Cydonia Slope, also within one percent, another 1/100 probability. It would be unfair if we ignored the very issue which brought us to the Face -- the question of artistic intent. Just how probable is it that a rock should look like a face? The question actually has a quantifiable answer. A face is composed of several features, details like eyes, a nose, ears, lips, a chin, and so on. Unless these features are represented by markings, an image won't look like a face. For a sculpture to look like a face, the artist must carve a depression for the eye sockets, and add a bulge for the nose, and so on. If a feature appears on a landform at a given location, there is only a 1/3 probability it will match aristic intent. That is, in the place where a sculptor would carve an eye socket, random nature might carve a depression -- or, it might leave the surface flat, or even place a projection. Likewise, for a nose, the artistic intent would place a projection at the center of a sculpture -- but nature could well leave a depression, or flat area, spoiling the artistic effect. These three choices -- depression, flat, projection -- hold for all the facial features. So, for each feature, nature has only a 1/3 chance to mimic artistic intent. In the First Face, there are seven clearly identifiable features: a smooth crown, straight bangs, a smooth hairline, an eye socket, a nose, a mouth, and a chin. The individual probability for nature getting an item right, and making a depression/bulge/flat-surface where needed, is 1/3. What of the cumulative probability for the overall composition? The cumulative probability is found by multiplying the individual feature probabilities together. For seven items, this is: 1/3 x 1/3 x 1/3 x 1/3 x 1/3 x 1/3 x 1/3 = 1/2187. If anything, this number seems biased in favor of the critics. The reality is that the Face is so unique an object that it calls our attention even among the millions of surface features on the planet Mars. But here, we're saying that one out of every two thousand or so landforms on Mars resembles a face to the same striking degree as does the one and only Face. The Second Face also has seven readily identifiable facelike features: two eyes, an eyelid, a nose, a mouth, a chin, a smooth side. Again, there are seven features, so again the cumulative probability is 1/2187. Let's now review all the independent probabilities for the correspondences between the Cydonia Complex and our Martian Moon God Temple Hypothesis, and multiply them into a cumulative improbability: Distance of Phobos Rock 1/100 x Distance of Deimos Rock 1/100 x Deimos Latitude 1/100 x Axial Tilt Alignment 1/100 x Composition of First Face 1/2187 x Composition of Second Face 1/2187 = Cumulative probability: 1/478,000,000,000,000 That is, in order to randomly produce the features seen at Cydonia, nature would require nearly 500 trillion 'tries' to achieve the precision of correspondence we've discussed here. To produce a schematic diagram of the Martian moon system with the detail shown at Cydonia, you would need 500 trillion tries. But -- Mars only has 250,000 tries to offer! If we take the ratio of these two numbers, we get 500 trillion / 250,000 = 2,000,000,000. The probability that random forces alone generated the Cydonia Complex is 1 /2,000,000,000.
In the future, little children will ask, "Couldn't you tell by looking?" But who was just 'looking'? We all brought prejudices and fears along with us. The American public once reacted in hysteria to a radio broadcast which simulated a Martian invasion. The monuments seem to be saying the Martians are long gone -- but perhaps we're still fearful of that invasion. Maybe, if there's any wishful thinking at all over this issue, it comes from the side of skepticism. Do the skeptics have an objective probability analysis to offer?
Imagine a science fiction story out of a 1930s pulp magazine. The story is titled, "The Photograph." It's about an automated space probe that snaps a photograph of the ruins of an ancient Martian civilization and transmits the image back to Earth. The brilliant scientists of the day instantly recognize the significance -- and danger. The photograph is classified, for fear of public hysteria, but the news leaks out and immediately seizes tremendous international attention. Worst of all, fundamentalist religious types find their beliefs challenged, go into frenzied denial, and mount a public crusade against human space exploration. That's how we'd assume it would go. In reality, the great minds looked at the picture and laughed. It was publicly released, and largely ignored. And rather than fundamentalist religious types, it is the establishment scientists themselves who find that the photograph challenges their beliefs, who deny the obvious interpretation of the telemetry -- and who have in the end even crusaded against space exploration. Why did everything get turned upside down? |